今日も見に来てくださって、ありがとうございます。石川さんです。
最近、データサイエンティストの勉強を再開しました。前回も勉強したのですけど、再び登場してきて引っかかったので、ちょっとメモしておきます。
モンテカルロ法とは
モンテカルロ法とは、乱数を使って数値計算やシュミレーションの近似解を求める方法です。今回は、これを使ってπを求めました。
πの求め方
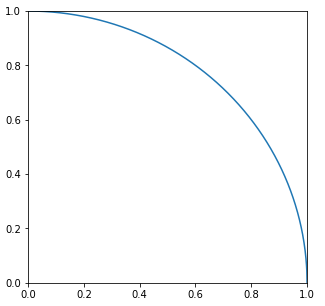
具体的には、1×1の正方形の中にランダムな点を打っていって、半径1の扇形の中に入る点と、入らない点に分けて、その比率を計算します。円の面積は、半径 × 半径 × πですので、この半径1の面積は、1 × 1 × π = πとなり、この扇形の面積はその四分の一になりますのでπ/4です。ここから扇形とこの正方形の比率より、π/4 : 1 = 内側の点の数 : すべての点の数という式が成り立ちます。この比例式からπ = 4 × 内側の点の数 / すべての点の数ということでπが算出できます。プログラムでランダムに10000個の点を打って、πの近似値を算出します。
ソースコード
import numpy as np import math from pandas import DataFrame r1 = np.random.uniform(0.0, 1.0, 10000) r2 = np.random.uniform(0.0, 1.0, 10000) p = DataFrame([(x, y) for x, y in zip(r1, r2) if math.hypot(x, y) < 1]) print(4 * len(p) / 10000)
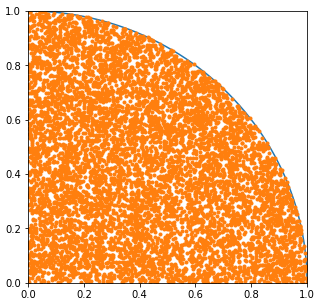
ぼくの環境で5回実行した結果は、3.1292、3.1384、3.15、3.168、3.1356という感じでした。まあまあ近いですね。回数を増やせば精度が上がっていくと思います。
あ、ソースコードの方、ちょっと説明をすると、np.random.uniform(始点,終点,個数)は、始点から終点までの一様乱数を個数で指定された数発生します。一様乱数とは、範囲の数値が等確率で乱数のことです。今回のこの例では、10000個の乱数を発生させています。そして、math.hypot(x,y)は、ユークリッド距離、つまり√(x*x+y*y)を計算した結果を返します。つまり、この関数で原点からx,y座標で指定した点までの距離が1より小さいかどうかを判定できます。
この結果を使ってデータをプロットしてみます。上の半径1の扇形を出力したスクリプトに追記してみます。
import numpy as np import matplotlib.pyplot as plt x = np.arange(0.0,2.0,0.001) y = np.sqrt(1-x**2) plt.figure(figsize=(5,5)) plt.xlim(0.0,1.0) plt.ylim(0.0,1.0) plt.plot(x,y) plt.plot(p[0],p[1],'.')
まとめ
モンテカルロ法、乱数を使って近似値を求められるなんて、ちょっとカッコいいですよね!