見に来てくださって、ありがとうございます。石川さんです。
先日、とある勉強会で、Pythonを使って1から10までの合計を出す、ということをやっていたのですが、自分でも解答を作ってみました。宿題は10個考えてくる、ということだったので、ぼくも10個、考えてみました。
あとで、実行時間を検証するために関数にしています。
解答と結果1
In [1]: def a1(N=10):
...: return 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
...: print("解答1:", a1())
解答1: 55
解説1
10個作らなきゃ、ということで真っ先に思いついたのがこれです。単純に足し算で足した結果を戻しています。1から10までの合計を算出する、という点においては合格ですが、関数としては、汎用性がなくてイマイチですね。合計が50までとか、10000まで、と変化した場合には使えません。そういう意味で、模範解答には遠いですね。
解答と結果2
In [2]: def a2(N=10):
...: s = 0
...: for i in range(1, N+1):
...: s += i
...: return s
...: print("解答2:", a2())
解答2: 55
解説2
次に思いついたのが、これですね。たぶん、いちばんオーソドックスなやつでは、と、思います。forループを使って繰り返し実行しますが、等差数列が必要なときは、組み込み関数のrange()を使用します。パラメータを二つ指定していますが、ひとつめの1は、初期値で1から始める、という意味です。ふたつめのN+1は、N+1のひとつ前の数字まで繰り返す、という意味です。これで、1から始めて11のひとつまえの10まで繰り返すことができます。
forループの構文の最後に指定するものは、イテラブルオブジェクトといって、反復可能なオブジェクトを指定します。具体的には、リストや文字列などはイテラブルオブジェクトで、繰り返し扱うための要素を複数持っているオブジェクトのことです。forループで指定されると、その要素をひとつずつ処理することができます。
ここで使用されている組み込み関数のrange()は、パラメータで指定された数のシーケンスで、イテラブルオブジェクトになります。もっと簡単に言うと、次の整数の値を順番に返してくれるオブジェクト、ということです。一般に、forループにおいて特定の回数の繰り返し処理に使われます。文章よりも実際の戻り値を確認してもらった方が早いと思いますので、まずは実行結果をご覧ください。
In [1]: range(3).__iter__()
Out[1]: <range_iterator at 0x26faa394f50>
In [2]: i = range(3).__iter__()
In [3]: i.__next__()
Out[3]: 0
In [4]: i.__next__()
Out[4]: 1
In [5]: i.__next__()
Out[5]: 2
In [6]: i.__next__()
Traceback (most recent call last):
File "<ipython-input-6-aa5506447029>", line 1, in <module>
i.__next__()
StopIteration
In [7]:
まずは、forループの最後の要素はイテラブルオブジェクトですので、__iter__()が呼び出されて、イテレータが取得されます。Out[1]から「range(3).__iter__()」の戻り値がrange_iteratorオブジェクトということがわかります。イテレータは__next__()を呼び出すことで次の要素を戻すという約束のあるオブジェクトです。ここで__next__()を呼び出すと、順番に、0、1、2を戻していますね。In [6]の、最後3を戻すかというところで、StopIterationの例外を発生します。forループはイテレータがStopIterationが発生するまで繰り返される、というお約束になっています。このようにして、要素の数分の繰り返し処理が実行されています。
ちなみに、__iter__()や__next__()などの特殊メソッドの部分は以下のように書き換えることもできます。
In [7]: i = iter(range(3))
In [8]: next(i)
Out[8]: 0
In [9]: next(i)
Out[9]: 1
In [10]: next(i)
Out[10]: 2
In [11]: next(i)
Traceback (most recent call last):
File "<ipython-input-11-a883b34d6d8a>", line 1, in <module>
next(i)
StopIteration
In [12]:
この特殊メソッドについて理解が進むと、Pythonでのプログラミングがより効率的にできるようになって、もっと楽しくなってくるのでは、と思います。
解答と結果3
def a3(N=10):
s = 0
for i in range(N):
s += (i + 1)
return s
print("解答3:", a3())
解答3: 55
解説3
解答2の類似で、0から始めて9までの10回繰り返す、というループで合計値を変えるパターンですね。そんなに違いはありませんがすべての繰り返しで足し算をしている分、遅いかもしれません。
解答と結果4
In [4]: def a4(N=10):
...: s = i = 0
...: while i < N:
...: i += 1
...: s += i
...: return s
...: print("解答4:", a4())
解答4: 55
解説4
Pythonで使える繰り返しもうひとつの繰り返し構文にwhileがあります。二行目で変数、sとiにそれぞれ0を代入して初期化しています。whileループの右側に条件が書いてありますが、この条件がTrue、真のあいだ、このループは繰り返されます。条件を書き間違えると無限にループしますので、注意が必要です。
4行目の「i += 1」は、iに1を加えた値をまたiに代入する、という意味で、iが1から始まってひとつずつ増えていくことになります。5行目の「s += i」は、sにiを加えた値を代入していきますので、この行が合計部分の処理をしていると言っていいでしょう。
解答と結果5
In [5]: def a5(N=10):
...: s = 0
...: while N > 0:
...: s += N
...: N -= 1
...: return s
...: print("解答5:", a5())
解答5: 55
解説5
解説4は1から10までという順番で加えていきましたが、今回は、10から1までという順番で加算するところが違いますね。5行目の「N -= 1」で1ずつ減算しているところがポイントでしょうか。
解答と結果6
In [6]: def a6(N=10):
...: s = 0
...: for i in range(N,0,-1):
...: s += i
...: return s
...: print("解答6:", a6())
解答6: 55
解説6
解説5をやって、range()の場合の逆順の加算を忘れていたことに気づきました。range()の第三引数に-1を指定することで、1ずつ減算していくことが可能です。まあ、a2、a3と、たいして変わりませんね。range()の使い方が異なるだけです。
解答と結果7
In [7]: def a7(N=10):
...: if N == 1:
...: return 1
...: return N + a7(N - 1)
...: print("解答7:", a7())
解答7: 55
解説7
これは、再帰呼び出しを利用した解答です。再帰呼び出しとは、関数の中で、自分自身の関数を呼び出すことをいいます。これにより繰り返し処理が可能になるプログラミング上のテクニックです。ポイントは4行目で、Nと自分自身を「N – 1」のパラメータで呼び出したときの戻り値を加算しているところです。呼び出された関数は、「N – 1」と自分自身を「(N – 1) – 1」で呼び出した値を戻して、と、次々と呼び出され、2行目の条件、Nが1になるまで再帰的に呼び出しが繰り返され、Nから1までの合計が求まります。
このテクニックの若干の問題は、関数呼び出しを何度も繰り返すところです。関数が呼び出されると呼び出した関数はスタックというところへ積み上げられます。呼び出された関数の処理が終了するまではそこで待機、というイメージですね。これのどこに問題があるのか、というと、このスタックの上限が整数値と比べると割と小さめに設定されている点です。
1000回では問題なく実行できましたが、10000回を指定するとエラーになってしまいました。
File "<ipython-input-4-124a61628543>", line 4, in a7
return N + a7(N - 1)
File "<ipython-input-4-124a61628543>", line 4, in a7
return N + a7(N - 1)
File "<ipython-input-4-124a61628543>", line 2, in a7
if N == 1:
RecursionError: maximum recursion depth exceeded in comparison
RecursionErrorということで、再帰エラーですね。調べてみると、こちらで現在値を確認できるようです。
In [8]: import sys In [9]: sys.getrecursionlimit() Out[9]: 3000
現在の値は3000でしたね。sys.setrecursionlimit()を使うことでセットもできるようですが、長くなりますので、今回はそこまで検証しませんね。
ちなみに、return文のところへif文を記述すると、関数内は以下の一行で記述できました。ちょっぴりだけスマートな感じがしますね。
return N + a7(N - 1) if N > 1 else 1
解答と結果8
def a8(N=10):
return N * (N + 1) // 2
print("解答8:", a8())
解答8: 55
解説8
これは、等差数列の合計を求める公式です。いつも公式が覚えられないので、以下の画像のような長方形の面積を考えてから、それの半分、というふうにして公式を導き出しています。下の場合、(1+10)×10が長方形の面積になって、その半分が求める合計ですね。これからN×(N+1)÷2の公式を導き出しています。
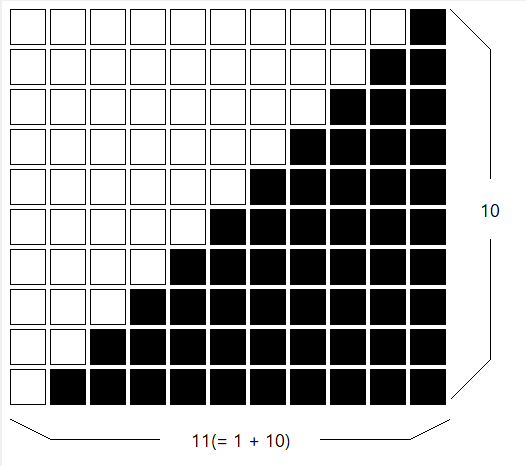
ぼくの予想では、この式を使って答えを出力するのが一番効率がよいのでは、というふうに思いました。他の処理の計算量はO(N)(Nに比例する)なのですが、この式の計算量はNの大きさによらないので、O(1)(定数)となります。
解答と結果9
In [9]: def a9(N=10):
...: return sum(range(N+1))
...: print("解答9:", a9())
解答9: 55
解説9
実は、宿題になる前に思いついたのがこのやり方です。Pythonだと、今回やりたいことは1行で完成します。はい、アルゴリズムの勉強にはなりませんね。
解答と結果10
In [10]: import numpy as np
...: def a10(N=10):
...: return np.sum(np.arange(N+1))
...: print("解答10:", a10())
解答10: 55
解説10
こちらもひとつ前のa9()と同じですが、numpyのライブラリを利用しています。大量データを扱うライブラリが豊富なnumpyですが、こちらの処理速度はいかがでしょうか。
まとめ
さて、最後になりますが、ここで紹介したロジックは、どれを使うのが正解なのでしょうか。どれを使っても結果はでるし、今回のロジックはどれも時間がかかるものではありませんので、いずれも正解です。結論から言うと、思いついたものですばやく実装する、もしくは、後で見たときにわかりやすい実装にする、というので問題ないでしょうね。あ、a1は、ダメですよ。
でも、プロとしてどのように実装するのが正解なのか、という指針を持っておきたい、という声が聞こえてきそうですね。指針のひとつとして、処理速度を計測しておきたいと思います。IPythonには%timeitというマジックコマンドがあって、いい感じに実行速度を測ってくれます。
In [11]: for f in [a1, a2, a3, a4, a5, a6, a7, a8, a9, a10]:
...: print(f.__name__, "=", f(), ":", end="")
...: %timeit f()
a1 = 55 :67.2 ns ± 3.61 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)
a2 = 55 :753 ns ± 51.7 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
a3 = 55 :842 ns ± 56.8 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
a4 = 55 :799 ns ± 145 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
a5 = 55 :801 ns ± 109 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
a6 = 55 :699 ns ± 43 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
a7 = 55 :1.23 µs ± 33.7 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
a8 = 55 :131 ns ± 4.65 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)
a9 = 55 :509 ns ± 19.1 ns per loop (mean ± std. dev. of 7 runs, 1000000 loops each)
a10 = 55 :3.48 µs ± 34.1 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
a1は参考値ですが、いちばん速いですね。1から10までの計算ではそんなに差が出ませんが、再帰処理のa7とnumpyの処理がちょっと遅いようです。ちょっと1から1000までの計算で測定しなおしてみます。
In [12]: for f in [a1, a2, a3, a4, a5, a6, a7, a8, a9, a10]:
...: print(f.__name__, "=", f(1000), ":", end="")
...: %timeit f(1000)
a1 = 55 :78.2 ns ± 4.14 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)
a2 = 500500 :51 µs ± 3 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
a3 = 500500 :78.4 µs ± 4.88 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
a4 = 500500 :85.7 µs ± 6.29 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
a5 = 500500 :104 µs ± 13 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
a6 = 500500 :51.7 µs ± 3.34 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
a7 = 500500 :177 µs ± 26.8 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
a8 = 500500 :188 ns ± 15.5 ns per loop (mean ± std. dev. of 7 runs, 10000000 loops each)
a9 = 500500 :16.4 µs ± 1.3 µs per loop (mean ± std. dev. of 7 runs, 100000 loops each)
a10 = 500500 :4.76 µs ± 162 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)
やはり最初の見立て通り、a8の公式を使った処理が最速で、Nの大きさによらないパフォーマンスですね。そして、a7の再帰処理、遅いですね。そしてnumpyを使ったa10は、10回と1000回でそんなに差が出ないという面白い結果になりました。大量データを扱うための工夫がありそうですね。あと、a2とa3は予想通り、a3の方が若干遅めですね。
ごらんの通り、遅いと言ってもすべて1ミリ秒以内で完了しているので、今回のケースでは、ほとんど誤差、と考えても差し支えないでしょうね。
(1秒=1,000ミリ秒=1,000,000マイクロ秒=1,000,000,000ナノ秒)
1から10までの合計を出すだけでも、いろいろなやり方があって、面白いですね!